堆

什么是堆？

堆（Heap）是一个可以被看成近似完全二叉树的数组。

• 堆是一个完全二叉树。完全二叉树要求，除了最后一层，其他层的节点个数都是满的，最后一层的节点都靠左排列。
• 堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点的值。

堆可以分为大顶堆和小顶堆。

• 对于每个节点的值都大于等于子树中每个节点值的堆，叫作“大顶堆”。

• 对于每个节点的值都小于等于子树中每个节点值的堆，叫作“小顶堆”。

如何实现堆

完全二叉树比较适合用数组来存储。用数组来存储完全二叉树是非常节省存储空间的。因为我们不需要存储左右子节点的指针，单纯地通过数组的下标，就可以找到一个节点的左右子节点和父节点。

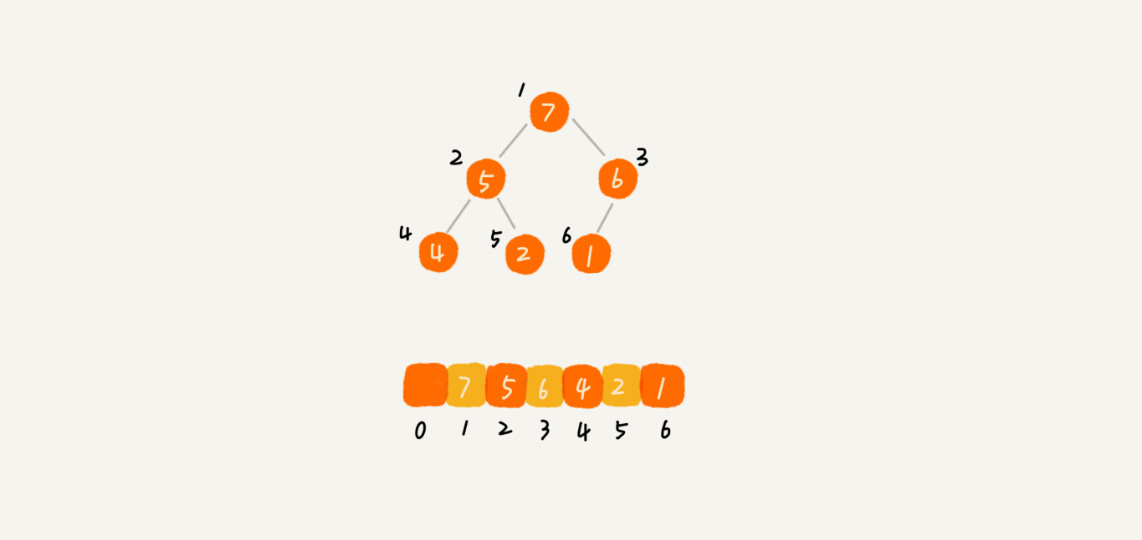
堆常见的操作：

• HEAPIFY 建堆：把一个乱序的数组变成堆结构的数组，时间复杂度为 $$O(n)$$。
• HEAPPUSH：把一个数值放进已经是堆结构的数组中，并保持堆结构，时间复杂度为 $$O(log N)$$
• HEAPPOP：从最大堆中取出最大值或从最小堆中取出最小值，并将剩余的数组保持堆结构，时间复杂度为 $$O(log N)$$。
• HEAPSORT：借由 HEAPFY 建堆和 HEAPPOP 堆数组进行排序，时间复杂度为$$ O(N log N)$$，空间复杂度为 $$O(1)$$。

堆的应用场景

求 TOP N

堆结构的一个常见应用是建立优先队列（Priority Queue）。

求 Top K 的问题抽象成两类。一类是针对静态数据集合；另一类是针对动态数据集合

优先级队列

在优先级队列中，数据的出队顺序不是先进先出，而是按照优先级来，优先级最高的，最先出队。

堆和优先级队列非常相似：往优先级队列中插入一个元素，就相当于往堆中插入一个元素；从优先级队列中取出优先级最高的元素，就相当于取出堆顶元素。

参考：Java 的 PriorityQueue 类

求中位数