技术文档规范
技术文档规范
文档采用 Markdown 语法书写。
📚 “参考”Markdown 语法可以参考:
1. 标题
1.1. 标题层级
标题分为四级。
- 一级标题:文章的标题
- 二级标题:文章内容的大标题
- 三级标题:二级标题下一级的标题
- 四级标题:三级标题下一级的标题
1.2. 标题原则
- 一篇文章中应该尽力避免同名标题。
- 一级标题下,不能直接出现三级标题。
- 标题要避免孤立编号(即同级标题只有一个)。
- 下级标题不重复上一级标题的内容。
- 谨慎使用四级标题,尽量避免出现,保持层级的简单和防止出现过于复杂的章节。如果三级标题下有并列性的内容,建议只使用项目列表(Item list)。
2. 文本
2.1. 字间距
全角中文字符与半角英文字符之间,应有一个半角空格。
1 | 反例:本文介绍如何快速启动Windows系统。 |
全角中文字符与半角阿拉伯数字之间,有没有半角空格都可,但必须保证风格统一,不能两种风格混杂。
1 | 正例:2011年5月15日,我订购了5台笔记本电脑与10台平板电脑。 |
半角的百分号,视同阿拉伯数字。
英文单位若不翻译,单位前的阿拉伯数字与单位间不留空格。
1 | 反例:一部容量为 16 GB 的智能手机 |
半角英文字符和半角阿拉伯数字,与全角标点符号之间不留空格。
1 | 反例:他的电脑是 MacBook Air 。 |
2.2. 句子
- 避免使用长句。一个句子建议不超过 100 字或者正文的 3 行。
- 尽量使用简单句和并列句,避免使用复合句。
2.3. 写作风格
尽量不使用被动语态,改为使用主动语态。
1 | 反例:假如此软件尚未被安装, |
不使用非正式的语言风格。
1 | 反例:Lady Gaga 的演唱会真是酷毙了,从没看过这么给力的表演!!! |
用对“的”、“地”、“得”。
1 | 她露出了开心的笑容。 |
使用代词时(比如“其”、“该”、“此”、“这”等词),必须明确指代的内容,保证只有一个含义。
1 | 反例:从管理系统可以监视中继系统和受其直接控制的分配系统。 |
名词前不要使用过多的形容词。
1 | 反例:此设备的使用必须在接受过本公司举办的正式的设备培训的技师的指导下进行。 |
单个句子的长度尽量保持在 20 个字以内;20 ~ 29 个字的句子,可以接受;30 ~ 39 个字的句子,语义必须明确,才能接受;多于 40 个字的句子,在任何情况下都不能接受。
1 | 反例:本产品适用于从由一台服务器进行动作控制的单一节点结构到由多台服务器进行动作控制的并行处理程序结构等多种体系结构。 |
同样一个意思,尽量使用肯定句表达,不使用否定句表达。
1 | 反例:请确认没有接通装置的电源。 |
避免使用双重否定句。
1 | 反例:没有删除权限的用户,不能删除此文件。 |
2.4. 英文处理
英文原文如果使用了复数形式,翻译成中文时,应该将其还原为单数形式。
1 | 英文:⋯information stored in random access memory (RAMs)⋯ |
外文缩写可以使用半角圆点(.)表示缩写。
1 | U.S.A. |
表示中文时,英文省略号(⋯)应改为中文省略号(……)。
1 | 英文:5 minutes later⋯ |
英文书名或电影名改用中文表达时,双引号应改为书名号。
1 | 英文:He published an article entitled "The Future of the Aviation". |
第一次出现英文词汇时,在括号中给出中文标注。此后再次出现时,直接使用英文缩写即可。
1 | IOC(International Olympic Committee,国际奥林匹克委员会)。这样定义后,便可以直接使用“IOC”了。 |
专有名词中每个词第一个字母均应大写,非专有名词则不需要大写。
1 | “American Association of Physicists in Medicine”(美国医学物理学家协会)是专有名词,需要大写。 |
3. 段落
3.1. 段落原则
- 一个段落只能有一个主题,或一个中心句子。
- 段落的中心句子放在段首,对全段内容进行概述。后面陈述的句子为核心句服务。
- 一个段落的长度不能超过七行,最佳段落长度小于等于四行。
- 段落的句子语气要使用陈述和肯定语气,避免使用感叹语气。
- 段落之间使用一个空行隔开。
- 段落开头不要留出空白字符。
3.2. 引用
引用第三方内容时,应注明出处。
1 | One man’s constant is another man’s variable. — Alan Perlis |
如果是全篇转载,请在全文开头显著位置注明作者和出处,并链接至原文。
1 | 本文转载自 WikiQuote |
使用外部图片时,必须在图片下方或文末标明来源。
1 | 本文部分图片来自 Wikipedia |
3.3. 强调
一些特殊的强调内容可以按照如下方式书写:
🔔 “注意”
💡 “提示”
📚 “参考”
4. 数值
4.1. 半角数字
数字一律使用半角形式,不得使用全角形式。
1 | 反例: 这件商品的价格是1000元。 |
4.2. 千分号
数值为千位以上,应添加千分号(半角逗号)。
1 | XXX 公司的实收资本为 RMB1,258,000。 |
对于 4 ~ 6 位的数值,千分号是选用的,比如1000和1,000都可以接受。对于 7 位及以上的数值,千分号是必须的。
多位小数要从小数点后从左向右添加千分号,比如4.234,345。
4.3. 货币
货币应为阿拉伯数字,并在数字前写出货币符号,或在数字后写出货币中文名称。
1 |
|
4.4. 数值范围
表示数值范围时,用~连接。参见《标点符号》一节的“连接号”部分。
带有单位或百分号时,两个数字都要加上单位或百分号,不能只加后面一个。
1 | 反例:132~234kg |
4.5. 变化程度的表示法
数字的增加要使用“增加了”、“增加到”。“了”表示增量,“到”表示定量。
1 | 增加到过去的两倍 |
数字的减少要使用“降低了”、“降低到”。“了”表示增量,“到”表示定量。
1 | 降低到百分之八十 |
不能用“降低 N 倍”或“减少 N 倍”的表示法,要用“降低百分之几”或“减少百分之几”。因为减少(或降低)一倍表示数值原来为一百,现在等于零。
5. 符号
5.1. 符号原则
- 中文语句的标点符号,均应该采取全角符号,这样可以保证视觉的一致。
- 如果整句为英文,则该句使用英文/半角标点。
- 句号、问号、叹号、逗号、顿号、分号和冒号不得出现在一行之首。
5.2. 句号
中文语句中的结尾处应该用全角句号(。)。
句子末尾用括号加注时,句号应在括号之外。
1 | 反例:关于文件的输出,请参照第 1.3 节(见第 26 页。) |
5.3. 逗号
逗号,表示句子内部的一般性停顿。
注意避免“一逗到底”,即整个段落除了结尾,全部停顿都使用逗号。
5.4. 顿号
句子内部的并列词,应该用全角顿号(、) 分隔,而不用逗号,即使并列词是英语也是如此。
1 | 反例:我最欣赏的科技公司有 Google, Facebook, 腾讯, 阿里和百度等。 |
英文句子中,并列词语之间使用半角逗号(,)分隔。
1 | 例句:Microsoft Office includes Word, Excel, PowerPoint, Outlook and other components. |
5.5. 分号
分号;表示复句内部并列分句之间的停顿。
5.6. 引号
引用时,应该使用全角双引号(“ ”),注意前后双引号不同。
1 | 例句:许多人都认为客户服务的核心是“友好”和“专业”。 |
引号里面还要用引号时,外面一层用双引号,里面一层用单引号(‘ ’),注意前后单引号不同。
1 | 例句:鲍勃解释道:“我要放音乐,可萨利说,‘不行!’。” |
5.7. 圆括号
补充说明时,使用全角圆括号(),括号前后不加空格。
1 | 例句:请确认所有的连接(电缆和接插件)均安装牢固。 |
5.8. 冒号
全角冒号(:)常用在需要解释的词语后边,引出解释和说明。
1 | 例句:请确认以下几项内容:时间、地点、活动名称,以及来宾数量。 |
表示时间时,应使用半角冒号(:)。
1 | 例句:早上 8:00 |
5.9. 省略号
省略号……表示语句未完、或者语气的不连续。它占两个汉字空间、包含六个省略点,不要使用。。。或...等非标准形式。
省略号不应与“等”这个词一起使用。
1 | 反例:我们为会餐准备了香蕉、苹果、梨…等各色水果。 |
5.10. 感叹号
应该使用平静的语气叙述,尽量避免使用感叹号!。
不得多个感叹号连用,比如!!和!!!。
5.11. 破折号
破折号————一般用于做进一步解释。破折号应占两个汉字的位置。
1 | 例句:直觉————尽管它并不总是可靠的————告诉我,这事可能出了些问题。 |
5.12. 连接号
连接号用于连接两个类似的词。
以下场合应该使用直线连接号(-),占一个半角字符的位置。
- 两个名词的复合
- 图表编号
1 | 例句:氧化-还原反应 |
以下场合应该使用波浪连接号(~),占一个全角字符的位置。
- 数值范围(例如日期、时间或数字)
1 | 例句:2009 年~2011 年 |
注意,波浪连接号前后两个值都应该加上单位。
波浪连接号也可以用汉字“至”代替。
1 | 例句:周围温度:-20°C 至 -10°C |
6. 结构
6.1. 目录结构
技术手册目录结构是一部完整的书,建议采用下面的结构。
- 简介(Introduction) - [必选][目录|文件] 提供对产品和文档本身的总体的、扼要的说明
- 入门篇(Quickstart) - [可选][文件] 如何最快速地使用产品
- 基础篇(Basics) - [必选][目录] 又称”使用篇“,提供初级的使用教程
- 环境准备(Prerequisite) - [可选][文件] 软件使用需要满足的前置条件
- 安装(Installation) - [可选][文件] 软件的安装方法
- 配置(Configuration) - [可选][目录|文件] 软件的配置
- 特性(Feature) - [必选][目录|文件] 软件的功能特性
- 进阶篇(Advanced) - [可选][目录] 又称”开发篇“,提供中高级的开发教程
- 原理(Principle) - [可选][目录|文件] 软件的原理
- 设计(Design) - [可选][目录|文件] 软件的设计,如:架构、设计思想等
- 实战篇(Action) - [可选][目录] 提供一些具有实战意义的示例说明
- API(API) - [可选][目录|文件] 软件 API 的逐一介绍
- 常见问题(FAQ) - [可选][目录|文件] 常见问题解答
- 附录(Appendix) - [可选][目录] 不属于教程本身、但对阅读教程有帮助的内容
- 命令(Command) - [可选][目录] 命令
- 资源(Resource) - [必选][文件] 资源
- 术语(Glossary) - [可选][文件] 名词解释
- 技巧(Recipe) - [可选][文件] 最佳实践
- 版本(Changelog) - [可选][文件] 版本说明
- 反馈(Feedback) - [可选][文件] 反馈方式
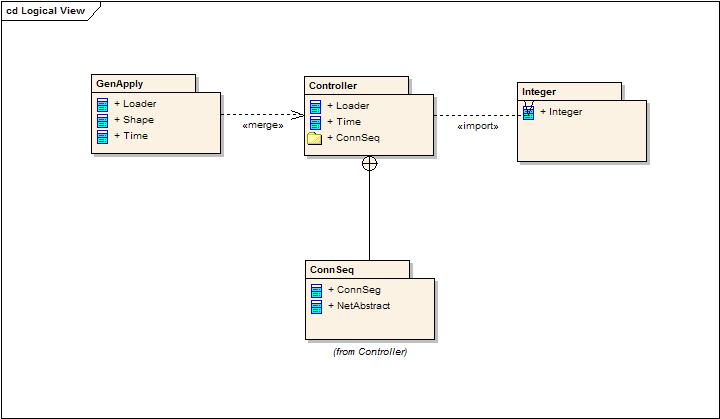
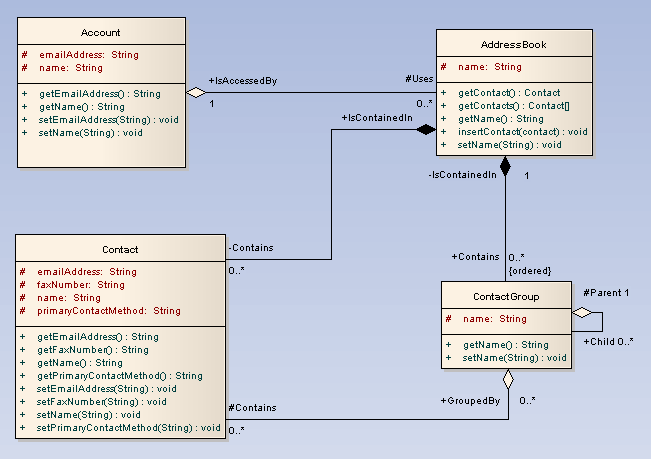
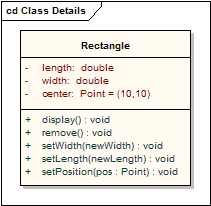
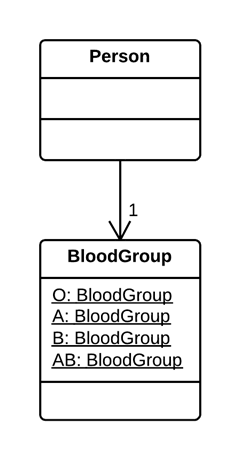
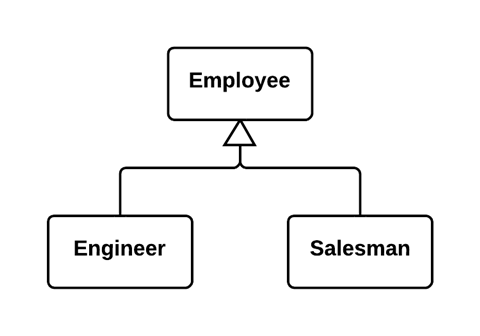
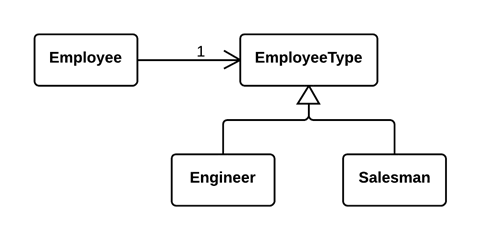
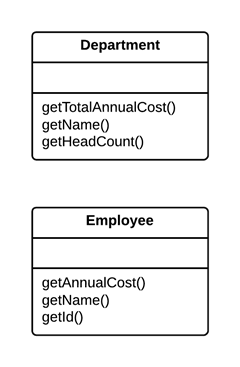
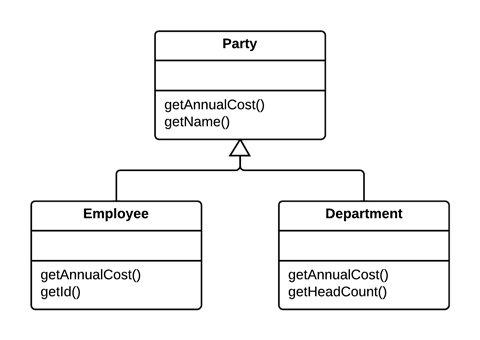
下面是两个真实范例,可参考。
6.2. 文件名
文档的文件名不得含有空格。
文件名必须使用半角字符,不得使用全角字符。这也意味着,中文不能用于文件名。
1 | 反例: 名词解释.md |
文件名建议只使用小写字母,不使用大写字母。
1 | 反例:TroubleShooting.md |
为了醒目,某些说明文件的文件名,可以使用大写字母,比如README、LICENSE。
文件名包含多个单词时,单词之间建议使用半角的连词线(-)分隔。
1 | 反例:advanced_usage.md |
7. Emoji
在 markdown 文档中,普遍会使用 emoji,帮助理解内容。但是,如果滥用 emoji,可能会适得其反。
这里,将一些比较约定俗成的 emoji 表情使用场景列举一下:
- 💡 提示 - [推荐]
- 🔔 注意、警告 - [推荐]
- ⭕ 正确 - [推荐]
- ❌ 错误 - [推荐]
- ❓ 问题 - [推荐]
- ⛔ 禁止 - [推荐]
- 🚧 未完待续、有待补充 - [推荐]
- 📚 参考、参考资料 - [可选]
- ⌨ 源码 - [可选]
8. 参考
- 产品手册中文写作规范, by 华为
- 写作规范和格式规范, by DaoCloud
- 技术写作技巧在日汉翻译中的应用, by 刘方
- 简体中文规范指南, by lengoo
- 文档风格指南, by LeanCloud
- 豌豆荚文案风格指南, by 豌豆荚
- 中文文案排版指北, by sparanoid
- 中文排版需求, by W3C
- 为什么文件名要小写?, by 阮一峰