网络协议之 ICMP

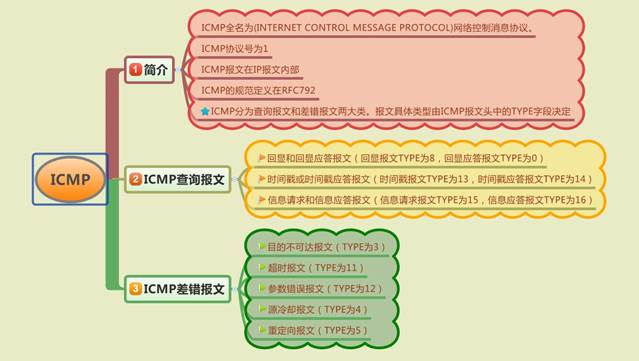
ICMP 简介

ICMP 全名为(INTERNET CONTROL MESSAGE PROTOCOL)网络控制消息协议。

ICMP 的协议号为1。

ICMP 报文就像是 IP 报文的小弟，总顶着 IP 报文的名头出来混。因为 ICMP 报文是在 IP 报文内部的，如图：

ICMP 类型

ICMP 报文主要有两大功能：查询报文和差错报文。

目的不可达(Destination Unreachable Message)

0 1 2 3

0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Type | Code | Checksum |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| unused |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Internet Header + 64 bits of Original Data Datagram |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

日常生活中，邮寄包裹会经过多个传递环节，任意一环如果无法传下去，都会返回寄件人，并附上无法邮寄的原因。同理，当路由器收到一个无法传递下去的 IP 报文时，会发送 ICMP目的不可达报文（Type 为 3）给 IP 报文的源发送方。报文中的 Code 就表示发送失败的原因。

Code

0 = net unreachable;

1 = host unreachable;

2 = protocol unreachable;

3 = port unreachable;

4 = fragmentation needed and DF set;

5 = source route failed.

超时(Time Exceeded Message)

0 1 2 3

0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Type | Code | Checksum |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| unused |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Internet Header + 64 bits of Original Data Datagram |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

网络传输 IP 数据报的过程中，如果 IP 数据包的 TTL 值逐渐递减为 0 时，需要丢弃数据报。这时，路由器需要向源发送方发送 ICMP 超时报文(Type 为 11)，Code 为 0，表示传输过程中超时了。

一个 IP 数据报可能会因为过大而被分片，然后在目的主机侧把所有的分片重组。如果主机迟迟没有等到所有的分片报文，就会向源发送方发送一个 ICMP 超时报文，Code 为 1，表示分片重组超时了。

参数错误报文(Parameter Problem Message)

0 1 2 3

0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Type | Code | Checksum |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Pointer | unused |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Internet Header + 64 bits of Original Data Datagram |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

当路由器或主机处理数据报时，发现因为报文头的参数错误而不得不丢弃报文时，需要向源发送方发送参数错误报文(Type 为 12)。当 Code 为 0 时，报文中的 Pointer 表示错误的字节位置。

源冷却(Source Quench Message)

0 1 2 3

0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Type | Code | Checksum |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| unused |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Internet Header + 64 bits of Original Data Datagram |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

路由器在处理报文时会有一个缓存队列。如果超过最大缓存队列，将无法处理，从而丢弃报文。并向源发送方发一个 ICMP 源冷却报文(Type 为 4)，告诉对方：“嘿，我这里客满了，你迟点再来。”

重定向(Redirect Message)

0 1 2 3

0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Type | Code | Checksum |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Gateway Internet Address |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Internet Header + 64 bits of Original Data Datagram |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

想像一下，在公司中，有人来你的项目组问你某某某在哪儿。你一想，我们组没有这人啊。你肯定就会说，我们组没有这号人，你去其他组看看。当路由收到 IP 数据报，发现数据报的目的地址在路由表上没有，它就会发 ICMP 重定向报文(Type 为 5)给源发送方，提醒它想要发送的地址不在，去其他地方找找吧。

请求回显或回显应答(Echo or Echo Reply Message)

0 1 2 3

0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Type | Code | Checksum |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Identifier | Sequence Number |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Data …

+-+-+-+-+-

**Type(8)是请求回显报文(Echo)；Type(0)是回显应答报文(Echo Reply)**。

请求回显或回显应答报文属于查询报文。Ping 就是用这种报文进行查询和回应。

时间戳或时间戳请求(Timestamp or Timestamp Reply Message)

0 1 2 3

0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Type | Code | Checksum |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Identifier | Sequence Number |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Originate Timestamp |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Receive Timestamp |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Transmit Timestamp |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

时间戳报文是用来记录收发以及传输时间的报文。Originate Timestamp 记录的是发送方发送报文的时刻；Receive Timestamp记录的是接收方收到报文的时刻；Transmit Timestamp表示回显这最后发送报文的时刻。

信息请求或信息响应

0 1 2 3

0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Type | Code | Checksum |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

| Identifier | Sequence Number |

+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+

这种报文是用来找出一个主机所在的网络个数（一个主机可能会在多个网络中）。报文的 IP 消息头的目的地址会填为全 0，表示 this，源地址会填为源 IP 所在的网络 IP。

总结

图：ICMP 知识点思维导图

参考

• RFC792

树和二叉树

树

什么是树

在计算机科学中，树（英语：tree）是一种抽象数据类型（ADT）或是实现这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由 n（n>0）个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

它具有以下的特点：

• 每个节点都只有有限个子节点或无子节点。
• 树有且仅有一个根节点。
• 根节点没有父节点；非根节点有且仅有一个父节点。
• 每个非根节点可以分为多个不相交的子树。
• 树里面没有环路。

树的术语

• 节点的度：一个节点含有的子树的个数称为该节点的度；
• 树的度：一棵树中，最大的节点度称为树的度；
• 叶子节点或终端节点：度为零的节点；
• 非终端节点或分支节点：度不为零的节点；
• 父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；
• 子节点：一个节点含有的子树的根节点称为该节点的子节点；
• 兄弟节点：具有相同父节点的节点互称为兄弟节点；
• 堂兄弟节点：父节点在同一层的节点互为堂兄弟；
• 节点的祖先：从根到该节点所经分支上的所有节点；
• 子孙：以某节点为根的子树中任一节点都称为该节点的子孙。
• 森林：由 m（m>=0）棵互不相交的树的集合称为森林；

• 节点的高度：节点到叶子节点的最长路径。高度是从下往上度量。
• 节点的深度：根节点到该节点的最长路径。深度是从上往下度量。
• 节点的层次：节点的深度 + 1。
• 树的高度：根节点的高度。

树的性质

• 树中的节点数等于所有节点的度数加 1。
• 度为 m 的树中第 i 层上至多有 $$m^{i-1}$$ 个节点（$$i ≥ 1$$）。
• 高度为 h 的 m 次树至多有 $$(m^h-1)/(m-1)$$ 个节点。
• 具有 n 个节点的 m 次树的最小高度为 $$\log_m{(n(m-1)+1)}$$ 。

树的种类

无序树：树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树；

有序树：树中任意节点的子节点之间有顺序关系，这种树称为有序树；

• 二叉树：每个节点最多含有两个子树的树称为二叉树；
  • 完全二叉树：对于一颗二叉树，假设其深度为 d（d>1）。除了第 d 层外，其它各层的节点数目均已达最大值，且第 d 层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树；
• 满二叉树：所有叶节点都在最底层的完全二叉树；
• 平衡二叉树（AVL 树）：当且仅当任何节点的两棵子树的高度差不大于 1 的二叉树；
• 排序二叉树(二叉查找树（英语：Binary Search Tree))：也称二叉搜索树、有序二叉树；
• 霍夫曼树：带权路径最短的二叉树称为哈夫曼树或最优二叉树；
• B 树：一种对读写操作进行优化的自平衡的二叉查找树，能够保持数据有序，拥有多于两个子树。

二叉树

二叉树中的每个节点最多有两个子节点，分别是左子节点和右子节点。

二叉树的性质

1. 二叉树第 i 层上的结点数目最多为 2^i-1 (i≥1)。
2. 深度为 k 的二叉树至多有 2^k-1 个结点(k≥1)。
3. 包含 n 个结点的二叉树的高度至少为 **log₂(n+1)**。
4. 在任意一棵二叉树中，若终端结点的个数为 n0，度为 2 的结点数为 n2，则 n0=n2+1。

满二叉树

除了叶子节点之外，每个节点都有左右两个子节点，这种二叉树就叫作满二叉树。

完全二叉树

叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大，这种二叉树叫作完全二叉树。

特点：叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。显然，一棵满二叉树必定是一棵完全二叉树，而完全二叉树未必是满二叉树。

存储一棵二叉树，有两种方法，一种是基于指针或者引用的二叉链式存储法，一种是基于数组的顺序存储法。

二叉链式存储法

每个节点有三个字段，其中一个存储数据，另外两个是指向左右子节点的指针。

顺序存储法

如果节点 X 存储在数组中下标为 i 的位置，下标为 2 _ i 的位置存储的就是左子节点，下标为 2 _ i + 1 的位置存储的就是右子节点。反过来，下标为 i/2 的位置存储就是它的父节点。通过这种方式，我们只要知道根节点存储的位置（一般情况下，为了方便计算子节点，根节点会存储在下标为 1 的位置），这样就可以通过下标计算，把整棵树都串起来。

如果是非完全二叉树，其实会浪费比较多的数组存储空间。所以，如果某棵二叉树是一棵完全二叉树，那用数组存储无疑是最节省内存的一种方式。因为数组的存储方式并不需要像链式存储法那样，要存储额外的左右子节点的指针。这也是 为什么完全二叉树要求最后一层的子节点都靠左的原因。

二叉树的遍历

二叉树的遍历有三种方式：

• 前序遍历：对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树。
• 中序遍历：对于树中的任意节点来说，先打印它的左子树，然后再打印它本身，最后打印它的右子树。
• 后序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印这个节点本身。

二叉查找树

二叉查找树是二叉树中最常用的一种类型，也叫二叉搜索树。顾名思义，二叉查找树是为了实现快速查找而生的。不过，它不仅仅支持快速查找一个数据，还支持快速插入、删除一个数据。

二叉查找树要求，在树中的任意一个节点，其左子树中的每个节点的值，都要小于这个节点的值，而右子树节点的值都大于这个节点的值。

二叉查找树的查找

首先，我们看如何在二叉查找树中查找一个节点。我们先取根节点，如果它等于我们要查找的数据，那就返回。如果要查找的数据比根节点的值小，那就在左子树中递归查找；如果要查找的数据比根节点的值大，那就在右子树中递归查找。

二叉查找树的插入

如果要插入的数据比节点的数据大，并且节点的右子树为空，就将新数据直接插到右子节点的位置；如果不为空，就再递归遍历右子树，查找插入位置。同理，如果要插入的数据比节点数值小，并且节点的左子树为空，就将新数据插入到左子节点的位置；如果不为空，就再递归遍历左子树，查找插入位置。

二叉查找树的删除

第一种情况是，如果要删除的节点没有子节点，我们只需要直接将父节点中，指向要删除节点的指针置为 null。

第二种情况是，如果要删除的节点只有一个子节点（只有左子节点或者右子节点），我们只需要更新父节点中，指向要删除节点的指针，让它指向要删除节点的子节点就可以了。

第三种情况是，如果要删除的节点有两个子节点，这就比较复杂了。我们需要找到这个节点的右子树中的最小节点，把它替换到要删除的节点上。然后再删除掉这个最小节点，因为最小节点肯定没有左子节点（如果有左子结点，那就不是最小节点了），所以，我们可以应用上面两条规则来删除这个最小节点。

二叉查找树的时间复杂度

不管操作是插入、删除还是查找，**时间复杂度其实都跟树的高度成正比，也就是 O(log n)**。

二叉查找树的形态各式各样。比如这个图中，对于同一组数据，我们构造了三种二叉查找树。它们的查找、插入、删除操作的执行效率都是不一样的。图中第一种二叉查找树，根节点的左右子树极度不平衡，已经退化成了链表，所以查找的时间复杂度就变成了 O(n)。

为什么需要二叉查找树

第一，哈希表中的数据是无序存储的，如果要输出有序的数据，需要先进行排序。而对于二叉查找树来说，我们只需要中序遍历，就可以在 O(n) 的时间复杂度内，输出有序的数据序列。

第二，哈希表扩容耗时很多，而且当遇到散列冲突时，性能不稳定，尽管二叉查找树的性能不稳定，但是在工程中，我们最常用的平衡二叉查找树的性能非常稳定，时间复杂度稳定在 O(logn)。

第三，笼统地来说，尽管哈希表的查找等操作的时间复杂度是常量级的，但因为哈希冲突的存在，这个常量不一定比 logn 小，所以实际的查找速度可能不一定比 O(logn) 快。加上哈希函数的耗时，也不一定就比平衡二叉查找树的效率高。

第四，哈希表的构造比二叉查找树要复杂，需要考虑的东西很多。比如散列函数的设计、冲突解决办法、扩容、缩容等。平衡二叉查找树只需要考虑平衡性这一个问题，而且这个问题的解决方案比较成熟、固定。

最后，为了避免过多的散列冲突，哈希表装载因子不能太大，特别是基于开放寻址法解决冲突的哈希表，不然会浪费一定的存储空间。

参考资料

• 数据结构与算法之美

栈和队列

队列和栈都是操作受限的线性表：前者先进先出，后者先进后出。

栈

栈是什么

在 LIFO(后进先出) 数据结构中，将首先处理添加到队列中的最新元素。

栈是一个 LIFO(后进先出) 数据结构。栈是一种“操作受限”的线性表，只允许在一端插入和删除数据。通常，插入操作在栈中被称作入栈 push 。与队列类似，总是在堆栈的末尾添加一个新元素。但是，删除操作，退栈 pop ，将始终删除队列中相对于它的最后一个元素。

当某个数据集合只涉及在一端插入和删除数据，并且满足后进先出、先进后出的特性，我们就应该首选“栈”这种数据结构。

从栈的定义可以看出，栈只支持两个基本操作：入栈 push() 和 出栈 pop() ，也就是在栈顶插入一个数据和从栈顶删除一个数据。在入栈和出栈过程中，只需要一两个临时变量存储空间，所以空间复杂度是 O(1)。

栈既可以用数组来实现，也可以用链表来实现。用数组实现的栈，我们叫作顺序栈，用链表实现的栈，我们叫作链式栈。

为什么需要栈

相比数组和链表，栈只是对操作进行了限制，似乎并没有任何优势。为什么不直接使用数组或者链表？为什么还要用这个“操作受限”的“栈”呢？

特定的数据结构是对特定场景的抽象，而且，数组或链表暴露了太多的操作接口，操作上的确灵活自由，但使用时就比较不可控，自然也就更容易出错。

栈的应用场景

（1）函数调用栈

（2）表达式求值

（3）表达式匹配

可以借助栈来检查表达式中的括号是否匹配

队列

在 FIFO 数据结构中，将首先处理添加到队列中的第一个元素。

队列是典型的 FIFO 数据结构。插入（insert）操作也称作入队（enqueue），新元素始终被添加在队列的末尾。 删除（delete）操作也被称为出队（dequeue)。 你只能移除第一个元素。

什么是队列

队列：先进先出的线性表。

队列是一种“操作受限”的线性表，只允许在一端插入数据，在另一端删除数据。

队列的最基本操作：**入队 enqueue()，放一个数据到队列尾部；出队 dequeue()**，从队列头部取一个元素。

队列可以用数组来实现，也可以用链表来实现。用数组实现的队列叫作顺序队列，用链表实现的队列叫作链式队列。

队满的判断条件是 tail == n，队空的判断条件是 head == tail。

循环队列

循环队列是一种较为特殊的队列。

循环队列的要点是确定好 队空和队满的判定条件。

在用数组实现的非循环队列中，队满的判断条件是 (tail+1) % n == head，队空的判断条件是 head == tail。

为什么需要队列

为什么需要队列和为什么需要栈，是同样的道理，参考 为什么需要栈

队列的应用场景

（1）阻塞队列

阻塞队列其实就是在队列基础上增加了阻塞操作。简单来说，就是：

• 在队列为空的时候，从队头取数据会被阻塞。因为此时还没有数据可取，直到队列中有了数据才能返回；
• 如果队列已经满了，那么插入数据的操作就会被阻塞，直到队列中有空闲位置后再插入数据，然后再返回。

（2）并发队列

线程安全的队列我们叫作并发队列。最简单直接的实现方式是直接在 enqueue()、dequeue() 方法上加锁，但是锁粒度大并发度会比较低，同一时刻仅允许一个存或者取操作。实际上，基于数组的循环队列，利用 CAS 原子操作，可以实现非常高效的并发队列。这也是循环队列比链式队列应用更加广泛的原因。

参考资料

• 数据结构与算法之美
• Leetcode：栈和队列