数组和链表

数组和链表分别代表了连续空间和不连续空间的存储方式，它们是线性表（Linear List）的典型代表。其他所有的数据结构，比如栈、队列、二叉树、B+ 树等，实际上都是这两者的结合和变化。

数组

数组用 连续 的内存空间来存储数据。

数组的访问

数组元素的访问是以行或列索引的单一下标表示。

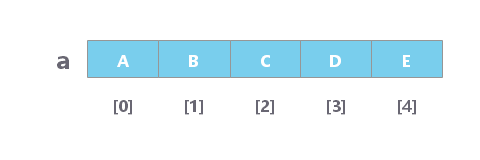
在上面的例子中，数组 a 中有 5 个元素。也就是说，a 的长度是 6 。我们可以使用 a[0] 来表示数组中的第一个元素。因此，a[0] = A 。类似地，a[1] = B，a[2] = C，依此类推。

数组的插入

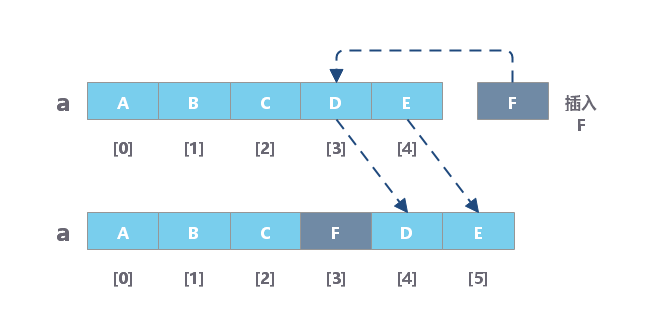
数组的删除

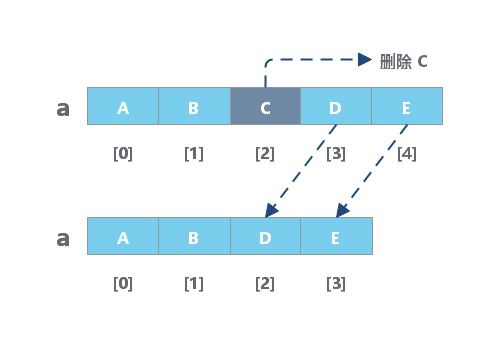
数组的特性

数组设计之初是在形式上依赖内存分配而成的，所以必须在使用前预先分配好空间大小。这使得数组有以下特性：

1. 用连续的内存空间来存储数据。
2. **数组支持随机访问，根据下标随机访问的时间复杂度为 O(1)**。
3. **数组的插入、删除操作，平均时间复杂度为 O(n)**。
4. 空间大小固定，一旦建立，不能再改变。扩容只能采用复制数组的方式。
5. 在旧式编程语言中（如有中阶语言之称的 C），程序不会对数组的操作做下界判断，也就有潜在的越界操作的风险。

多维数组

数组是有下标和值组成集合。

如果数组的下标有多个维度，即为多维数组。比如：二维数组可以视为“数组元素为一维数组”的一维数组；三维数组可以视为“数组元素为二维数组”的一维数组；依次类推。

下图是由 M 个行向量，N 个列向量组成的二维数组.

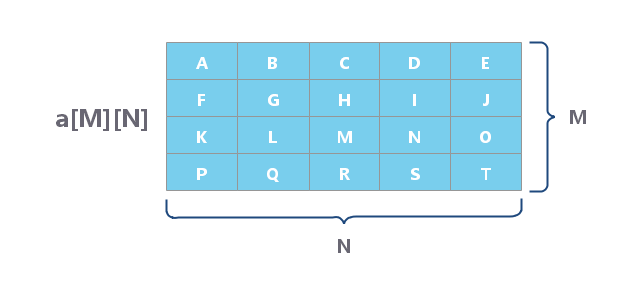
链表

链表用不连续的内存空间来存储数据；并通过一个指针按顺序将这些空间串起来，形成一条链。

区别于数组，链表中的元素不是存储在内存中连续的一片区域，链表中的数据存储在每一个称之为“结点”复合区域里，在每一个结点除了存储数据以外，还保存了到下一个节点的指针（Pointer）。由于不必按顺序存储，链表在插入数据的时候可以达到 O(1) 的复杂度，但是查找一个节点或者访问特定编号的节点则需要 O(n) 的时间。

链表具有以下特性：

• 链表允许插入和移除任意位置上的节点，其时间复杂度为 O(1)
• 链表没有数组的随机访问特性，链表只支持顺序访问，其时间复杂度为 O(n)。
• 数组的空间大小是固定的，而链表的空间大小可以动态增长。相比于数组，链表支持扩容，显然更为灵活，但是由于多了指针域，空间开销也更大。
• 链表相比于数组，多了头指针、尾指针（非必要），合理使用可以大大提高访问效率。

链表有多种类型：

• 单链表
• 双链表
• 循环链表

单链表

单链表中的每个结点不仅包含数据值，还包含一个指针，指向其后继节点。通过这种方式，单链表将所有结点按顺序组织起来。

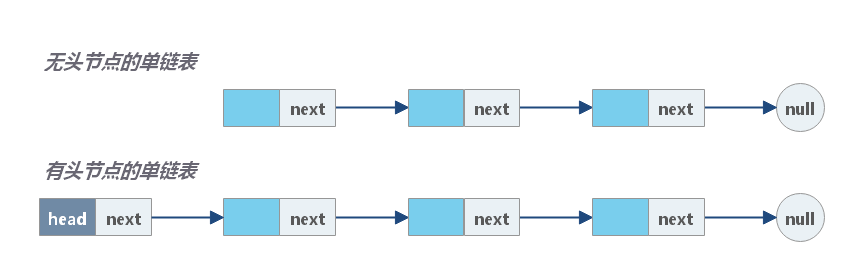
与数组不同，我们无法在常量时间内访问单链表中的随机元素。 如果我们想要获得第 i 个元素，我们必须从头结点逐个遍历。 我们按 索引 来 访问元素 平均要花费 O(N) 时间，其中 N 是链表的长度。

单链表插入

如果我们想在给定的结点 prev 之后添加新值，我们应该：

（1）使用给定值初始化新结点 cur；

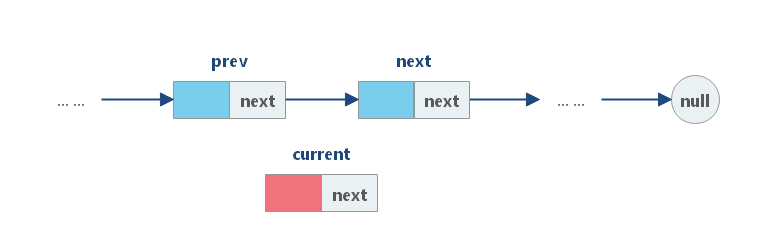
（2）将 cur 的 next 字段链接到 prev 的下一个结点 next ；

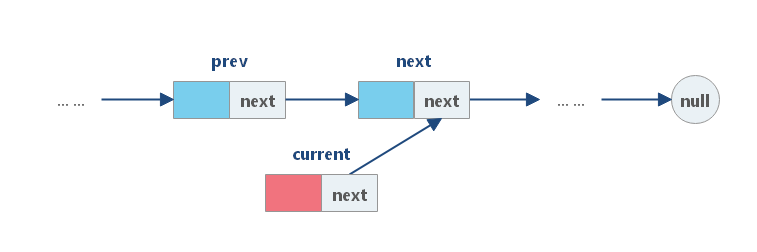
（3）将 prev 中的 next 字段链接到 cur 。

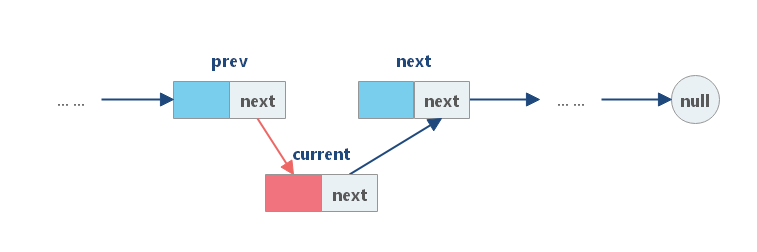
与数组不同，我们不需要将所有元素移动到插入元素之后。因此，您可以在 O(1) 时间复杂度中将新结点插入到链表中，这非常高效。

单链表删除

如果我们想从单链表中删除现有结点 cur，可以分两步完成：

（1）找到 cur 的上一个结点 prev 及其下一个结点 next ；

（2）接下来链接 prev 到 cur 的下一个节点 next 。

在我们的第一步中，我们需要找出 prev 和 next。使用 cur 的参考字段很容易找出 next，但是，我们必须从头结点遍历链表，以找出 prev，它的平均时间是 O(N)，其中 N 是链表的长度。因此，删除结点的时间复杂度将是 O(N)。

空间复杂度为 O(1)，因为我们只需要常量空间来存储指针。

双链表

双链表中的每个结点不仅包含数据值，还包含两个指针，分别指向指向其前驱节点和后继节点。

单链表的访问是单向的，而双链表的访问是双向的。显然，双链表比单链表操作更灵活，但是空间开销也更大。

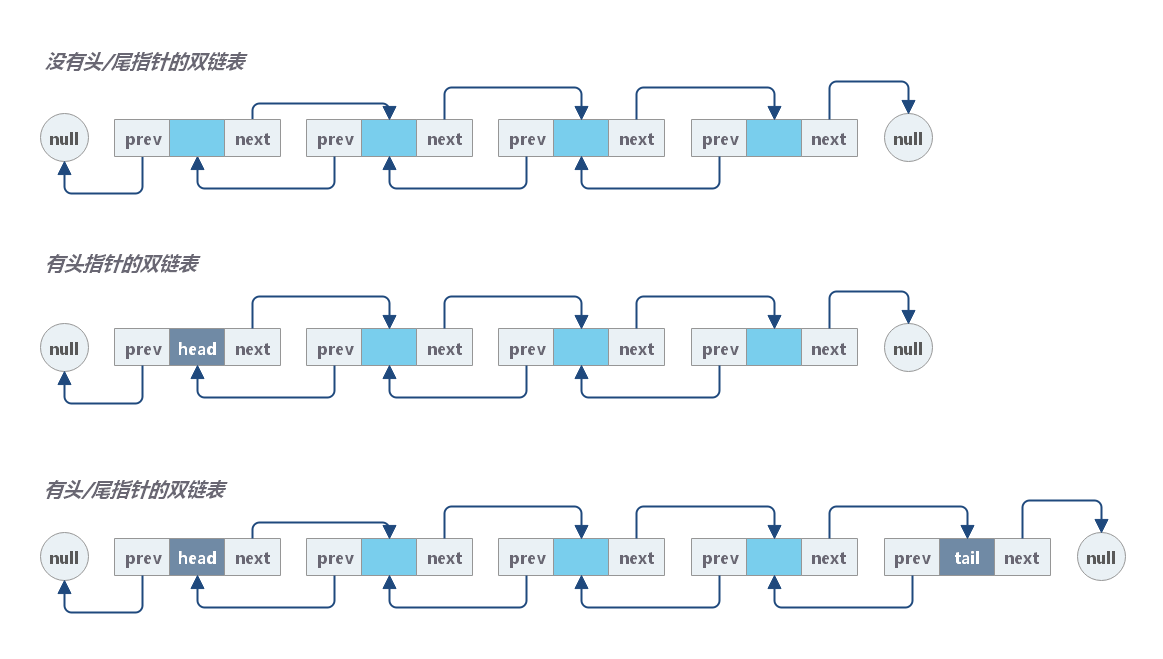
双链表以类似的方式工作，但还有一个引用字段，称为“prev”字段。有了这个额外的字段，您就能够知道当前结点的前一个结点。

双链表插入

如果我们想在给定的结点 prev 之后添加新值，我们应该：

（1）使用给定值初始化新结点 cur；

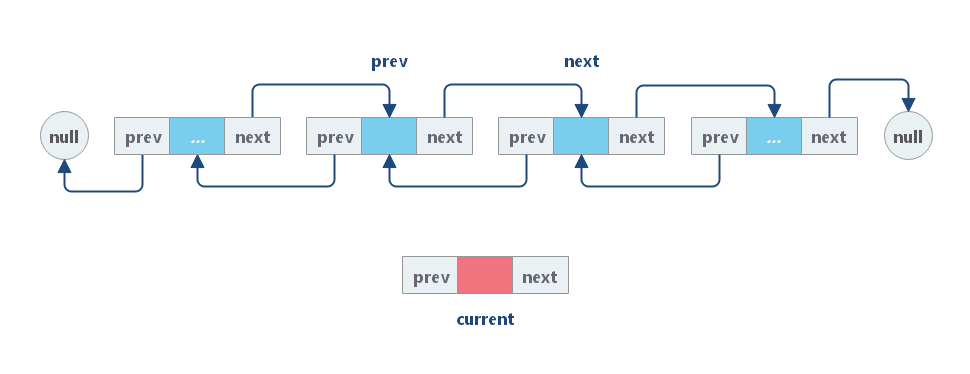
（2）链接 cur 与 prev 和 next，其中 next 是 prev 原始的下一个节点；

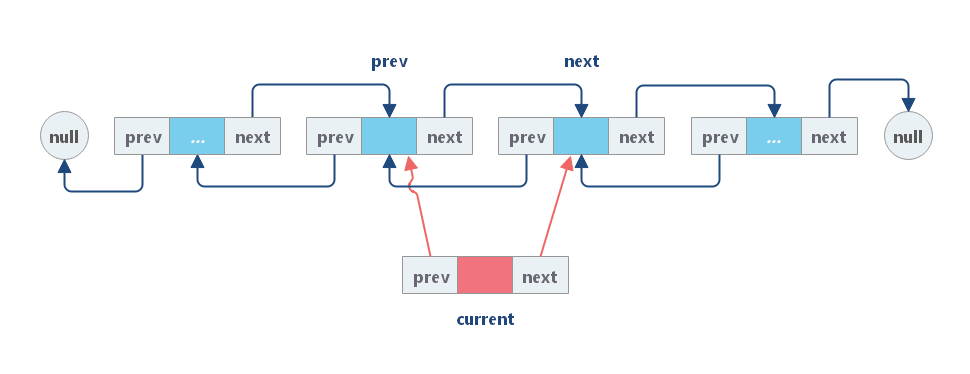
（3）用 cur 重新链接 prev 和 next。

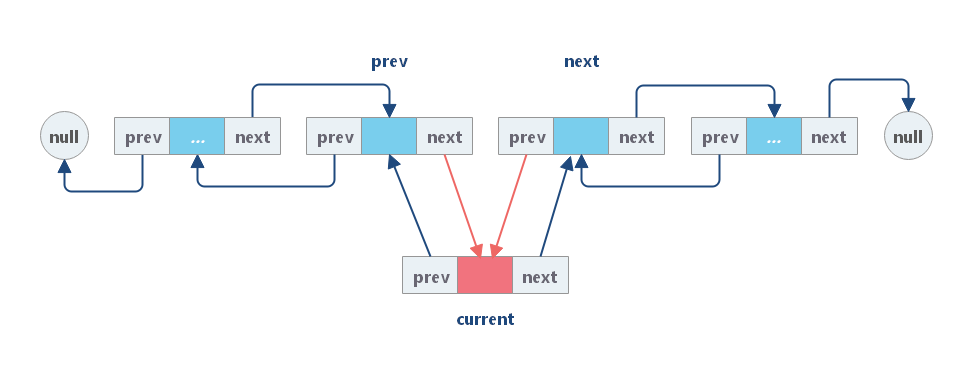
与单链表类似，添加操作的时间和空间复杂度都是 O(1)。

双链表删除

如果我们想从双链表中删除一个现有的结点 cur，我们可以简单地将它的前一个结点 prev 与下一个结点 next 链接起来。

与单链表不同，使用 prev 字段可以很容易地在常量时间内获得前一个结点。

因为我们不再需要遍历链表来获取前一个结点，所以时间和空间复杂度都是 O(1)。

循环链表

循环单链表

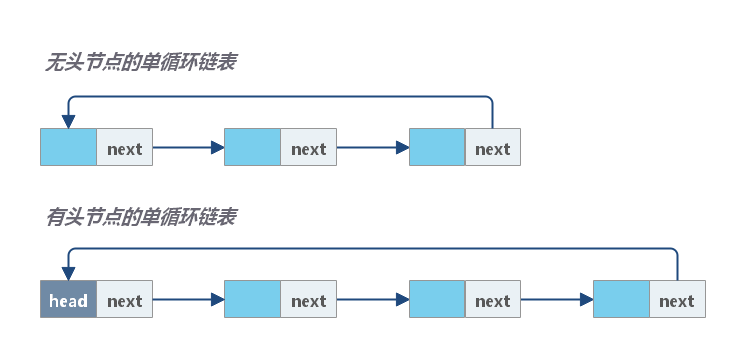
循环单链表是一种特殊的单链表。它和单链表唯一的区别就在最后结点。

• 单链表的最后一个结点的后继指针 next 指向空地址。
• 循环链表的最后一个结点的后继指针 next 指向第一个节点（如果有头节点，就指向头节点）。

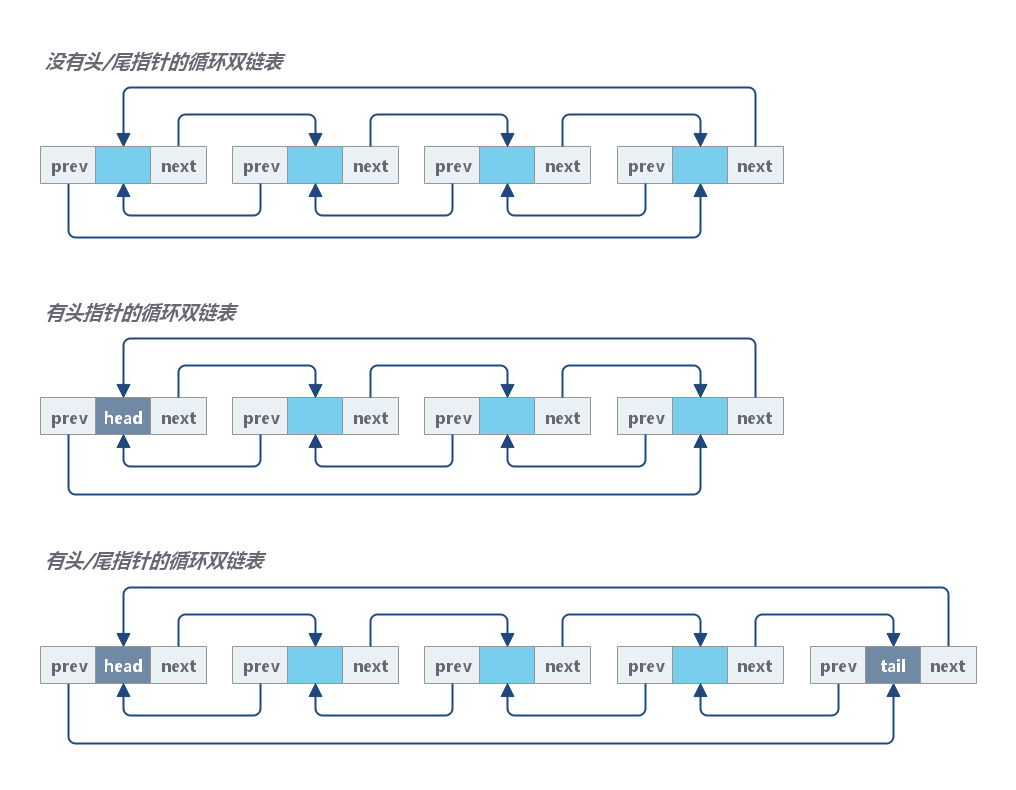
循环双链表

数组 vs. 链表

• 存储方式
  • 数组用 连续 的内存空间来存储数据。
  • 链表用 不连续 的内存空间来存储数据；并通过一个指针按顺序将这些空间串起来，形成一条链。
• 访问方式
  • 数组支持随机访问。根据下标随机访问的时间复杂度为 O(1)
  • 链表不支持随机访问，只能顺序访问，时间复杂度为 O(n)。
• 空间大小
  • 数组空间大小固定，扩容只能采用复制数组的方式。
  • 链表空间大小不固定，扩容灵活。
• 效率比较
  • 数组的 查找 效率高于链表。
  • 链表的 添加、删除 效率高于数组。

数组和链表的基本操作示例

关于数组和链表的基本操作，网上和各种书籍、教程中已经有大量的示例，感兴趣可以自行搜索。本文只是简单展示一下数组和链表的基本操作。

一维数组的基本操作

public class Main {
    public static void main(String[] args) {
        // 1. Initialize
        int[] a0 = new int[5];
        int[] a1 = {1, 2, 3};
        // 2. Get Length
        System.out.println("The size of a1 is: " + a1.length);
        // 3. Access Element
        System.out.println("The first element is: " + a1[0]);
        // 4. Iterate all Elements
        System.out.print("[Version 1] The contents of a1 are:");
        for (int i = 0; i < a1.length; ++i) {
            System.out.print(" " + a1[i]);
        }
        System.out.println();
        System.out.print("[Version 2] The contents of a1 are:");
        for (int item: a1) {
            System.out.print(" " + item);
        }
        System.out.println();
        // 5. Modify Element
        a1[0] = 4;
        // 6. Sort
        Arrays.sort(a1);
    }
}

二维数组的基本操作

public class TwoDimensionArray {
    private static void printArray(int[][] a) {
        for (int i = 0; i < a.length; ++i) {
            System.out.println(a[i]);
        }
        for (int i = 0; i < a.length; ++i) {
            for (int j = 0; a[i] != null && j < a[i].length; ++j) {
                System.out.print(a[i][j] + " ");
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        System.out.println("Example I:");
        int[][] a = new int[2][5];
        printArray(a);
        System.out.println("Example II:");
        int[][] b = new int[2][];
        printArray(b);
        System.out.println("Example III:");
        b[0] = new int[3];
        b[1] = new int[5];
        printArray(b);
    }
}

单链表的基本操作

单链表节点的数据结构

public class ListNode<E> {
    E value;
    ListNode<E> next; // 指向后继节点
}

public class SingleLinkList<E> {
    private ListNode<E> head; // 头节点
}

（1）从头部添加节点（即头插法）

void addHead(E value) {
    ListNode<E> newNode = new ListNode<>(value, null);
    newNode.next = this.head.next;
    this.head.next = newNode;
}

（2）从尾部添加节点（即尾插法）

void addTail(E value) {
    // init new node
    ListNode<E> newNode = new ListNode<>(value, null);

    // find the last node
    ListNode<E> node = this.head;
    while (node.next != null) {
        node = node.next;
    }

    // add new node to tail
    node.next = newNode;
}

（3）删除节点

找到要删除元素的前驱节点，将前驱节点的 next 指针指向下一个节点。

public void remove(E value) {
    ListNode<E> prev = this.head;
    while (prev.next != null) {
        ListNode<E> curr = prev.next;
        if (curr.value.equals(value)) {
            prev.next = curr.next;
            break;
        }
        prev = prev.next;
    }
}

（4）查找节点

从头开始查找，一旦发现有数值与查找值相等的节点，直接返回此节点。如果遍历结束，表明未找到节点，返回 null。

public ListNode<E> find(E value) {
    ListNode<E> node = this.head.next;
    while (node != null) {
        if (node.value.equals(value)) {
            return node;
        }
        node = node.next;
    }
    return null;
}

双链表的基本操作

双链表节点的数据结构：

static class DListNode<E> {
    E value;
    DListNode<E> prev; // 指向前驱节点
    DListNode<E> next; // 指向后继节点
}

public class DoubleLinkList<E> {
    /** 头节点 */
    private DListNode<E> head;
    /** 尾节点 */
    private DListNode<E> tail;
}

（1）从头部添加节点

public void addHead(E value) {
    DListNode<E> newNode = new DListNode<>(null, value, null);

    this.head.next.prev = newNode;
    newNode.next = this.head.next;

    this.head.next = newNode;
    newNode.prev = this.head;
}

（2）从尾部添加节点

public void addTail(E value) {
    DListNode<E> newNode = new DListNode<>(null, value, null);

    this.tail.prev.next = newNode;
    newNode.prev = this.tail.prev;

    this.tail.prev = newNode;
    newNode.next = this.tail;
}

（3）删除节点

public void remove(E value) {
    DListNode<E> prev = this.head;
    while (prev.next != this.tail) {
        DListNode<E> curr = prev.next;
        if (curr.value.equals(value)) {
            prev.next = curr.next;
            curr.next.prev = prev;
            curr.next = null;
            curr.prev = null;
            break;
        }
        prev = prev.next;
    }
}

（4）查找节点

public DListNode<E> find(E value) {
    DListNode<E> node = this.head.next;
    while (node != this.tail) {
        if (node.value.equals(value)) {
            return node;
        }
        node = node.next;
    }
    return null;
}

练习

• 数组
  • 724. 寻找数组的中心下标
  • 35. 搜索插入位置
  • 56. 合并区间
• 链表
  • 设计链表
  • 环形链表
  • 环形链表 II
  • 相交链表
  • 删除链表的倒数第 N 个节点
  • 反转链表
  • 移除链表元素
  • 奇偶链表
  • 回文链表
  • 合并两个有序链表
  • 两数相加
  • 扁平化多级双向链表
  • 复制带随机指针的链表
  • 旋转链表

参考资料

• 数据结构与算法之美
• 数据结构（C 语言版）
• 数据结构（C++语言版）
• Leetcode：数组和字符串
• Leetcode：链表