复杂度分析

发表于 更新于 分类于 ， 本文字数： 2.1k 阅读时长 ≈ 2 分钟

复杂度分析

为什么需要复杂度分析

衡量算法的优劣，有两种评估方式：事前估计和后期测试。

后期测试有性能测试、基准测试（Benchmark）等手段。

但是，后期测试有以下限制：

  • 测试结果非常依赖测试环境。如：不同机型、不同编译器版本、不同硬件配置等等，都会影响测试结果。
  • 测试结果受数据规模的影响很大。

所以，需要一种方法，可以不受环境或数据规模的影响，粗略地估计算法的执行效率。这种方法就是复杂度分析。

时间复杂度分析

大 O 表示法

假设问题的规模为 n，则程序的时间复杂度表示为 T(n)。代码的执行时间 T(n) 与每行代码的执行次数 n 成正比。

当 n 增大时，T(n) 也随之增大，想要准确估计其变化比较困难。所以，可以采用大 O 时间复杂度来粗略估计其复杂度，其表达式为：**T(n) = O(f(n))**。

大 O 表示法实际上并不具体表示代码真正的执行时间，而是表示代码执行时间随数据规模增长的变化趋势，所以，也叫作渐进时间复杂度（asymptotic time complexity），简称时间复杂度。

时间复杂度分析的要点

  • 只关注循环执行次数最多的一段代码
  • 加法法则：总复杂度等于量级最大的那段代码的复杂度
  • 乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

最好、最坏和平均情况

  • 最好情况时间复杂度（best case time complexity）：在最理想的情况下，执行代码的时间复杂度。例如：在最理想的情况下，要查找的变量 x 正好是数组的第一个元素，此时最好情况时间复杂度为 1。
  • 最坏情况时间复杂度（worst case time complexity）：在最糟糕的情况下，执行代码的时间复杂度。例如：在最理想的情况下，要查找的变量 x 正好是数组的最后个元素，此时最好情况时间复杂度为 n。
  • 平均情况时间复杂度（average case time complexity）：平均时间复杂度的全称应该叫加权平均时间复杂度或者期望时间复杂度。

时间复杂度分析示例

【示例】从 1 累加到 100 的时间复杂度是多少？

1
2
3
4
5
int sum = 0;
int N = 100;
for (int i = 1; i <= N; i++) {
    sum = sum + i;
}

时间复杂度计算：显然，这段代码执行了 100 次加法，其时间复杂度和 N 的大小完全一致

1
T(n) = O(n)

【示例】嵌套循环的时间复杂度是多少？

1
2
3
4
5
6
7
int M = 10;
int N = 20;
for (int i = 1; i < M; i++) {
    for (int j = 1; j < N; j++) {
        System.out.println("i = " + i + ", j = " + j);
    }
}

时间复杂度计算：

1
T(n) = (M-1)(N-1) = O(M*N) ≈ O(N^2)

【示例】递归函数的时间复杂度是多少？思考一下斐波那契数列 f(n) = f(n-1) + f(n-2) 的时间复杂度是多少？

img

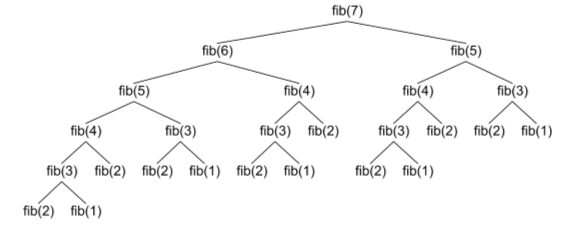
1
T(n) = O(2^N)

空间复杂度分析

时间复杂度的全称是渐进时间复杂度，表示算法的执行时间与数据规模之间的增长关系。

类比一下，空间复杂度全称就是渐进空间复杂度（asymptotic space complexity），表示算法的存储空间与数据规模之间的增长关系。

复杂度量级

复杂度有以下量级：

  • **O(1)**：常数复杂度
  • **O(log n)**：对数复杂度
  • **O(n)**：线性复杂度
  • **O(nlog n)**：线性对数阶复杂度
  • **O(n^2)**：平方复杂度
  • **O(n^3)**：立方复杂度
  • **O(n^k)**：K 次方复杂度
  • **O(2^n)**：指数复杂度
  • **O(n!)**：阶乘复杂度

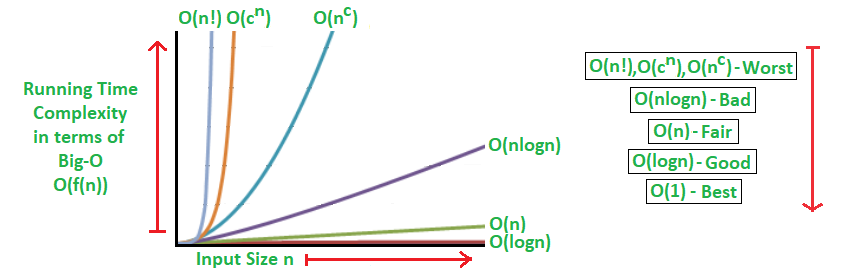
在数据量比较小的时候，复杂度量级差异并不明显；但是，随着数据规模大小的变化，差异会逐渐突出。

img

O(1) 复杂度示例：

1
2
int num = 100;
System.out.println("num = " + num);

O(log n) 对数复杂度示例：

1
2
3
4
int max = 100;
for (int i = 1; i < max; i = i * 2) {
    System.out.println("i = " + i);
}

O(n) 复杂度示例：

1
2
3
4
int max = 100;
for (int i = 1; i < max; i++) {
    System.out.println("i = " + i);
}

O(n^2) 复杂度示例：

1
2
3
4
5
6
7
int M = 10;
int N = 20;
for (int i = 1; i < M; i++) {
    for (int j = 1; j < N; j++) {
        System.out.println("i = " + i + ", j = " + j);
    }
}

O(k^n) 复杂度示例：

1
2
3
4
int max = 10;
for (int i = 1; i <= Math.pow(2, max); i++) {
    System.out.println("i = " + i);
}

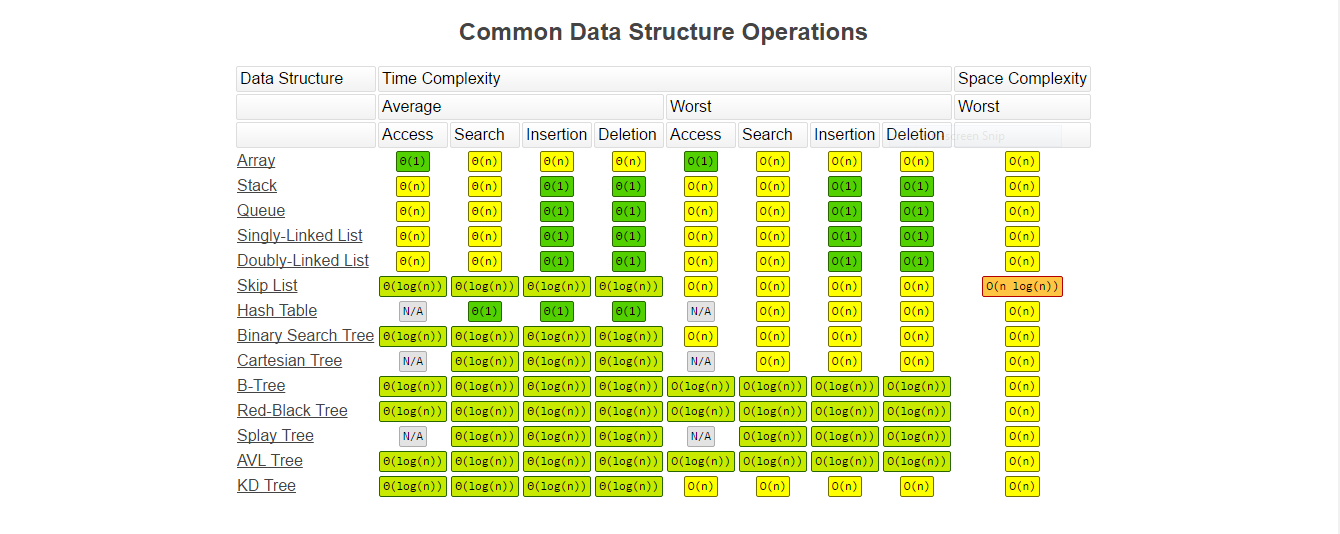
常见数据结构的复杂度

img

参考资料