字典树
字典树
什么是字典树
Trie 树(又叫“前缀树”或“字典树”)是一种用于快速查询“某个字符串/字符前缀”是否存在的数据结构。
- 根节点(Root)不包含字符,除根节点外的每一个节点都仅包含一个字符;
- 从根节点到某一节点路径上所经过的字符连接起来,即为该节点对应的字符串;
- 任意节点的所有子节点所包含的字符都不相同;
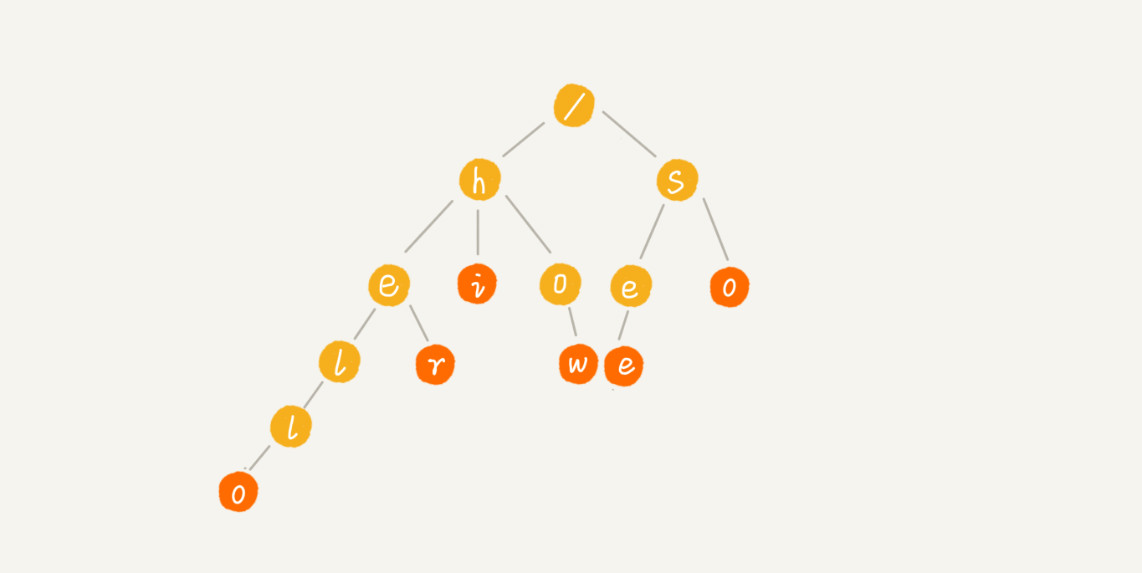
字典树的构造
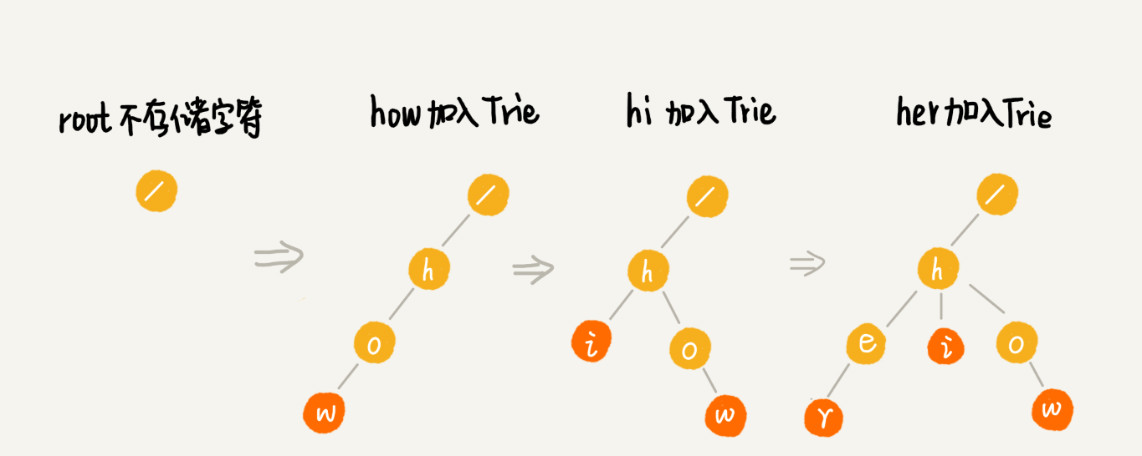
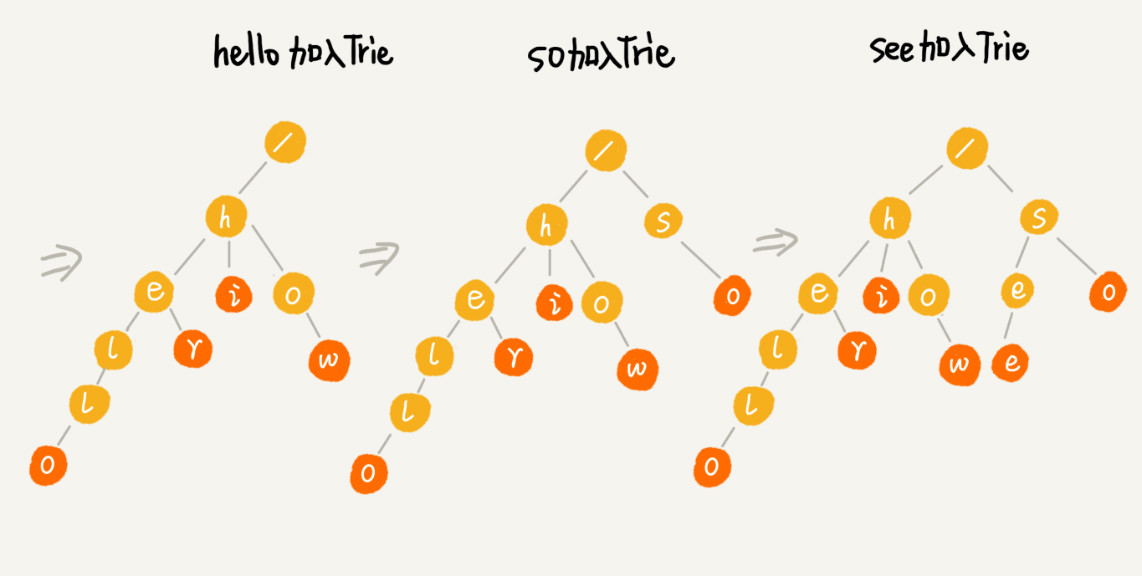
构建 Trie 树的过程,需要扫描所有的字符串,时间复杂度是 O(n)(n 表示所有字符串的长度和)。
字典树非常耗费内存。
用数组来存储一个节点的子节点的指针。如果字符串中包含从 a 到 z 这 26 个字符,那每个节点都要存储一个长度为 26 的数组,并且每个数组存储一个 8 字节指针(或者是 4 字节,这个大小跟 CPU、操作系统、编译器等有关)。而且,即便一个节点只有很少的子节点,远小于 26 个,比如 3、4 个,我们也要维护一个长度为 26 的数组。
用数组来存储一个节点的子节点的指针。如果字符串中包含从 a 到 z 这 26 个字符,那每个节点都要存储一个长度为 26 的数组,并且每个数组存储一个 8 字节指针(或者是 4 字节,这个大小跟 CPU、操作系统、编译器等有关)。而且,即便一个节点只有很少的子节点,远小于 26 个,比如 3、4 个,我们也要维护一个长度为 26 的数组。
用数组来存储一个节点的子节点的指针。如果字符串中包含从 a 到 z 这 26 个字符,那每个节点都要存储一个长度为 26 的数组,并且每个数组存储一个 8 字节指针(或者是 4 字节,这个大小跟 CPU、操作系统、编译器等有关)。而且,即便一个节点只有很少的子节点,远小于 26 个,比如 3、4 个,我们也要维护一个长度为 26 的数组。
字典树的查找
- 每次从根结点开始搜索;
- 获取关键词的第一个字符,根据该字符选择对应的子节点,转到该子节点继续检索;
- 在相应的子节点上,获取关键词的第二个字符,进一步选择对应的子节点进行检索;
- 以此类推,进行迭代过程;
- 在某个节点处,关键词的所有字母已被取出,则读取附在该节点上的信息,查找完成。
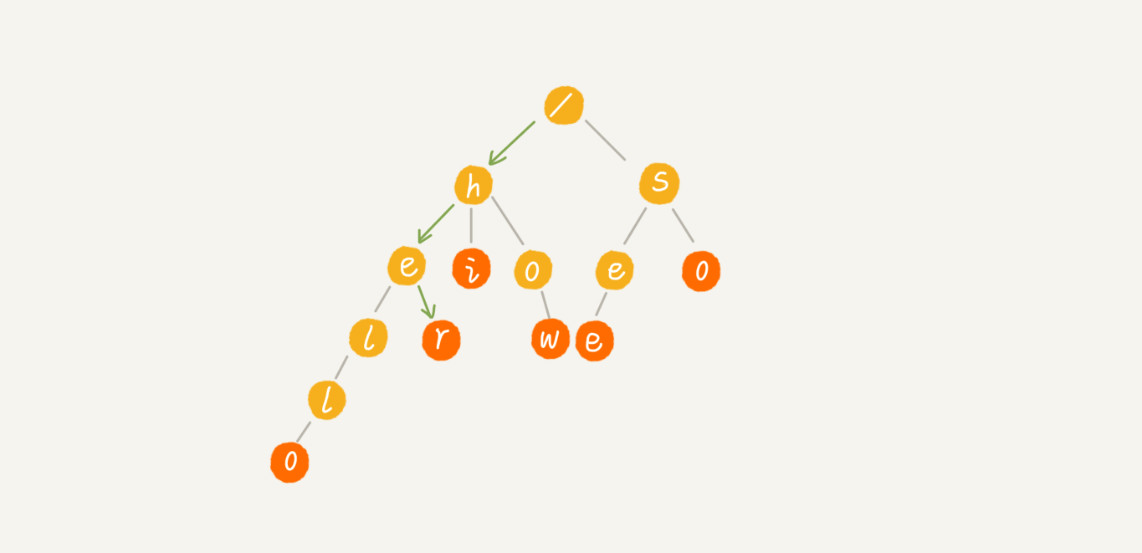
每次查询时,如果要查询的字符串长度是 k,那我们只需要比对大约 k 个节点,就能完成查询操作。跟原本那组字符串的长度和个数没有任何关系。所以说,构建好 Trie 树后,在其中查找字符串的时间复杂度是 O(k),k 表示要查找的字符串的长度。
字典树的应用场景
在一组字符串中查找字符串,Trie 树实际上表现得并不好。它对要处理的字符串有及其严苛的要求。
第一,字符串中包含的字符集不能太大。我们前面讲到,如果字符集太大,那存储空间可能就会浪费很多。即便可以优化,但也要付出牺牲查询、插入效率的代价。
第二,要求字符串的前缀重合比较多,不然空间消耗会变大很多。
第三,如果要用 Trie 树解决问题,那我们就要自己从零开始实现一个 Trie 树,还要保证没有 bug,这个在工程上是将简单问题复杂化,除非必须,一般不建议这样做。
第四,我们知道,通过指针串起来的数据块是不连续的,而 Trie 树中用到了指针,所以,对缓存并不友好,性能上会打个折扣。
在一组字符串中查找字符串,Trie 树实际上表现得并不好。它对要处理的字符串有及其严苛的要求。
在一组字符串中查找字符串,Trie 树实际上表现得并不好。它对要处理的字符串有及其严苛的要求。
(1)自动补全

(2)拼写检查
(3)IP 路由 (最长前缀匹配)
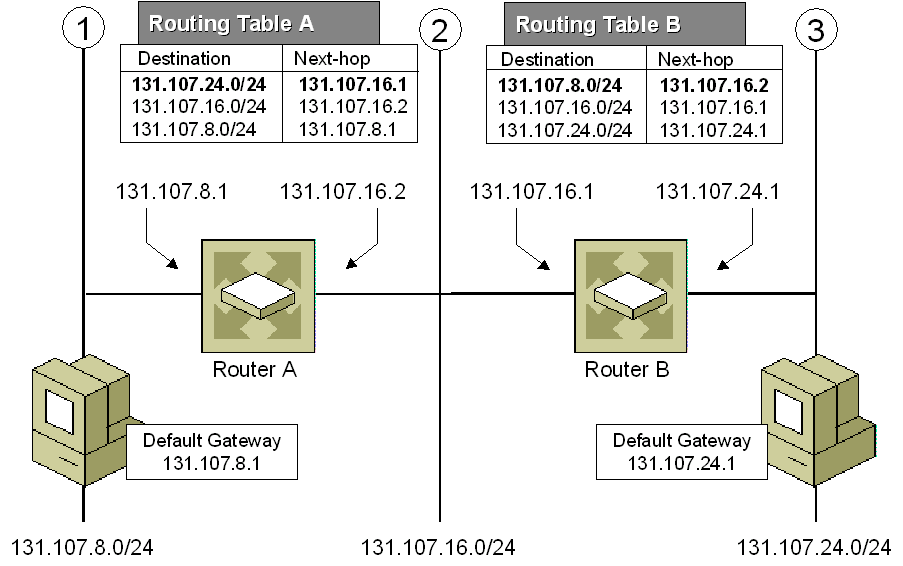
图 3. 使用 Trie 树的最长前缀匹配算法,Internet 协议(IP)路由中利用转发表选择路径。
(4)T9 (九宫格) 打字预测
(5)单词游戏

Trie 树可通过剪枝搜索空间来高效解决 Boggle 单词游戏